📘 Premium Read: Access my best content on Medium member-only articles — deep dives into Java, Spring Boot, Microservices, backend architecture, interview preparation, career advice, and industry-standard best practices.
✅ Some premium posts are free to read — no account needed. Follow me on Medium to stay updated and support my writing.
🎓 Top 10 Udemy Courses (Huge Discount): Explore My Udemy Courses — Learn through real-time, project-based development.
▶️ Subscribe to My YouTube Channel (172K+ subscribers): Java Guides on YouTube
Sorting is an algorithm that arranges the elements of a list in a certain order [either ascending or descending].
Bubble Sort Overview
Bubble sort is the simplest sorting algorithm. It works by iterating the input array from the first element to the last, comparing each pair of elements and swapping them if needed. Bubble sort continues its iterations until no more swaps are needed. This algorithm is not suitable for large datasets as its average and worst case complexity is of Ο(n2) where n is the number of items.
The only significant advantage that bubble sort has over other implementations is that it can detect whether the input list is already sorted or not.
How Bubble Sort Works?
We take an unsorted array for our example. Bubble sort takes Ο(n2) time so we're keeping it short and precise.
Bubble sort starts with very first two elements, comparing them to check which one is greater.
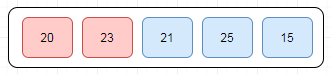
In this case, value 23 is greater than 20, so it is already in sorted locations. Next, we compare 23 with 21.
We find that 21 is smaller than 23 and these two values must be swapped.
The new array should look like this −
Next, we compare the 23 and 25. We find that both are in already sorted positions.
Then we move to the next two values, 25 and 15 -
We know then that 15 is smaller 25 and these values are not sorted. Let's swap these values and we find that we have reached the end of the array.
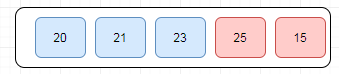
After the first iteration, the array should look like this −
To be precise, we are now showing how an array should look like after each iteration. After the second iteration, it should look like this −
Notice that after each iteration, at least one value moves at the end.
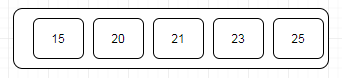
And when there's no swap required, bubble sorts learns that an array is completely sorted.
So far, we have seen what is bubble sort and how it works so now let's implement bubble sort using Java.
Bubble Sort Implementation
Let's write bubble sorting logic in three different ways such as iterative, recursively and optimized.
Iterative solution
// Simple logic using for loops
private void bubbleSort(int arr[]) {
int n = arr.length;
for (int i = 0; i < n - 1; i++)
for (int j = 0; j < n - i - 1; j++)
if (arr[j] > arr[j + 1]) {
// swap temp and arr[i]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
Recursive Solution
// recursive bubble sort
private void bubbleSort(int arr[], int n) {
// Base case
if (n == 1)
return;
// One pass of bubble sort. After
// this pass, the largest element
// is moved (or bubbled) to end.
for (int i = 0; i < n - 1; i++) {
if (arr[i] > arr[i + 1]) {
// swap arr[i], arr[i+1]
int temp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = temp;
}
}
// Largest element is fixed,
// recur for remaining array
bubbleSort(arr, n - 1);
}
Optimized Solution
The above logic for bubble sort algorithm takes O(n2) (even in best case). We can improve it by using one extra flag. No more swaps indicate the completion of sorting. If the list is already sorted, we can use this flag to skip the remaining passes.
// optimized
private void optimizedBubbleSort(int[] arr) {
int i = 0, n = arr.length;
boolean swapNeeded = true;
while (i < n - 1 && swapNeeded) {
swapNeeded = false;
for (int j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
int temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
swapNeeded = true;
}
}
if (!swapNeeded)
break;
i++;
}
}
This modified version improves the best case of bubble sort to O(n).
I will paste the complete program for your reference here.
Complete Program
import java.util.Arrays;
/**
* Class demonstrate the Bubble sorting algorithm
* @author Ramesh Fadatare
*
*/
public class BubbleSort {
// recursive bubble sort
private void bubbleSort(int arr[], int n) {
// Base case
if (n == 1)
return;
// One pass of bubble sort. After
// this pass, the largest element
// is moved (or bubbled) to end.
for (int i = 0; i < n - 1; i++) {
if (arr[i] > arr[i + 1]) {
// swap arr[i], arr[i+1]
int temp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = temp;
}
}
// Largest element is fixed,
// recur for remaining array
bubbleSort(arr, n - 1);
}
// Simple logic using for loops
private void bubbleSort(int arr[]) {
int n = arr.length;
for (int i = 0; i < n - 1; i++)
for (int j = 0; j < n - i - 1; j++)
if (arr[j] > arr[j + 1]) {
// swap temp and arr[i]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
// optimized
private void optimizedBubbleSort(int[] arr) {
int i = 0, n = arr.length;
boolean swapNeeded = true;
while (i < n - 1 && swapNeeded) {
swapNeeded = false;
for (int j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
int temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
swapNeeded = true;
}
}
if (!swapNeeded)
break;
i++;
}
}
public static void main(String[] args) {
final int[] arr = { 1, 4, 5, 6, 7, 8, 2, 3 };
final BubbleSort bubbleSort = new BubbleSort();
System.out.println("Before sorting the array elements : " + Arrays.toString(arr));
bubbleSort.bubbleSort(arr);
System.out.println("After sorting the array elements : " + Arrays.toString(arr));
bubbleSort.optimizedBubbleSort(arr);
System.out.println("After sorting the array elements order : " + Arrays.toString(arr));
bubbleSort.bubbleSort(arr, arr.length);
System.out.println("After sorting the array elements order : " + Arrays.toString(arr));
}
}
Output:
Before sorting the array elements : [1, 4, 5, 6, 7, 8, 2, 3]
After sorting the array elements : [1, 2, 3, 4, 5, 6, 7, 8]
After sorting the array elements order : [1, 2, 3, 4, 5, 6, 7, 8]
After sorting the array elements order : [1, 2, 3, 4, 5, 6, 7, 8]Performance
- Worst case complexity: O(n2)
- Best case complexity (Improved version): O(n)
- Average case complexity (Basic version): O(n2)
- Worst case space complexity: O(1) auxiliary
What do you use "swapNeeded" for?
ReplyDelete